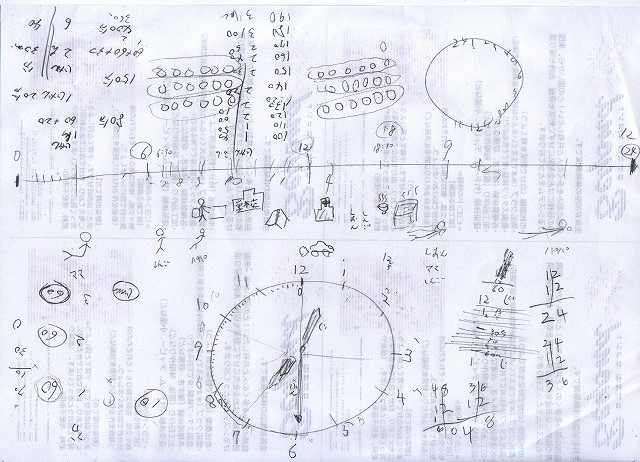
時計の読み方
小学校二年生の支温は、今、学校で時計の読み方を習っているらしい。
そして、宿題があるのだが解けないということで、ちょっと教えることにした。
“頑張って解こうとしているのだが、解けない“で困っている、、、
理解できていないから解けないのに、それを解こうと頑張っているのだ。
自分で解を見つけるということ自体は素晴らしいのだが、それは自分オリジナルの解が許される場合のこと。
一日が5時間かな? 1時間かな?なんて言うのは悩めば悩むほど、本当の解(とされるもの)を教わった時に覚えるのが”ややこしくなる。
”24時間だったっけ?いや、5時間だったかな?”
こういう勉強方法はどうも主流なのかもしれないが、非常に効率が低いと自分では感じる。大学受験の時にも周りの人の勉強方法を見て強く感じた。
ストレスを感じながらでは進みが遅いだけでなく、何よりもツマラナイ!
一日は24時間、一時間は60分、はい、覚えて!
というのでも良いが、ちょっと面白くはないな~
という事で、まずは『時間』という概念を教えることにした。
ママ起きる→支温起きる→朝ごはん→学校にいく→昼ご飯→ママ仕事終わる→支温帰宅→パパ畑から戻る→夕食→寝る
そして、誰かと会う約束をする時など、どのタイミングて会うかを決めるのに『時間』という指針があると便利だよねという話をした。
その際、一日を何分割するのがいいかを二人で考えた。
3分割だと荒すぎるし、100分割だと細かすぎるかな~
次に時計というものを見せた。一日は繰り返されるので、グルグル回って元に戻るのを時計の針で読めるようにしたら便利だよねという話も。
時計に印をつける時、一日が100時間とすると目盛りが細かすぎて読めないことがわかった。
じゃあ、何分割にしたらいいかな?
ケーキを切る時みたいに8分割だとやりやすいかな~。
しかし、12分割にしたほうが見た目にも良く、見やすかった。
じゃあ、一日を12時間にしようか!
時計から一日の流れを示した絵に目を戻すと、あれ?12分割だと説明しきれないね、、、
一日にやることの項目が全員分を足すと多すぎるため、分割をもう少し増やしたい、、、 でも、時計の分割はあまり増やしたくない(見難くなるから)、、
さて、じゃあ時計を二周で一日って言うことにしたらどうかな?
12+12で24時間。一日に7時というものが二回来ることになるね。
今これを朝の7時、夜の7時と呼ぶとすると、朝の7時は朝ごはん。夜の7時は夕ごはん。
ただ7時と言うと、どちらかわからないから、時計の読み方としては、一周目を午前、二周目を午後と呼ぶことにしたんだよ。
時計の針には長いのと短いのがあるね。
何でかな?
という感じに一つ一つ説明しながら、二人で時計を自作しながら考えた。
長い針があることで、短い針一つでは読み取りにくい細かい時間が簡単に読み取れることがわかったようだ。
そして、12の目盛りごとに5分割すると、5+5+、、、=60になることを教えた。
支温は実際に確かめたかったらしく、自分で足してみて60になることを確認し、更に自作した時計に目盛りを書き込んだ。
そう、興味を持てば自然に自分から確かめようとするんだこれ、重要^^
なんで3分割でなく、5分割?
これも自分でやってみればわかる。5分割のほうが十進法では表示がすっきりするんだよな。一の桁が5か0だけになるから。
一日が24時間というのも、ただ覚えるのではなく、理解していたとしたらテストに出ても簡単。
教室にかかっている時計を見れば12目盛り。二周で一日だから、12+12=24時間。自分で答えが求められる。
一時間は何分?12目盛りが5分割だから、60分。
実際に時計の目盛りや一日の時間などが自分の考えたように決められたかどうかは知らないが、そのように考えながらやるのは自分にとっては面白い。
概念がわかったら、後は何度も自分で使っているうちに勝手に覚えるだろう。
足し算、引き算
同じように、足し算、引き算でも宿題が解けずに困っていた時に少し教えたことがある。
問題にはただ解を出せと書いてある、、、
うーん、、、これでは足し算、引き算の概念を理解していない子供にはわからないだろうな、、、
コインを使い、実際に足し算や引き算をしてみた。
支温の好きなお店やさんごっこだ。
一円玉が増えすぎると数えるのが大変になるから、10円玉が必要になること。
10円玉がひとつ増える時、一円玉は10枚減ること(繰り上げ)、、、毎回10円玉に変えていると、一円玉は0~9枚までにしかならないこと、、、
繰り上げの際には、必ず10円玉は1枚しか増えないということ、、、
何度も繰り返すことで自然にわかってきたようだ。
さて、計算式が横書きだったので縦書に変換してみた。
一の位が1円玉、10の位が10円玉という関連性が見やすくなるから。
案の定、式を縦書にしたら意味がわかったらしい。
縦書の式とコインを共に使いながら計算を進めていくうち、コインを多く並べるのが大変であり、いきなり式に書いたほうが楽だということに自ら気づいたようだ!
あとはバンバン式を書いて渡すと、自分で喜んで解き出した^^
ストレスとなっていた内容の宿題が喜びに変わる、、、
どうせやるなら楽しくやろう~